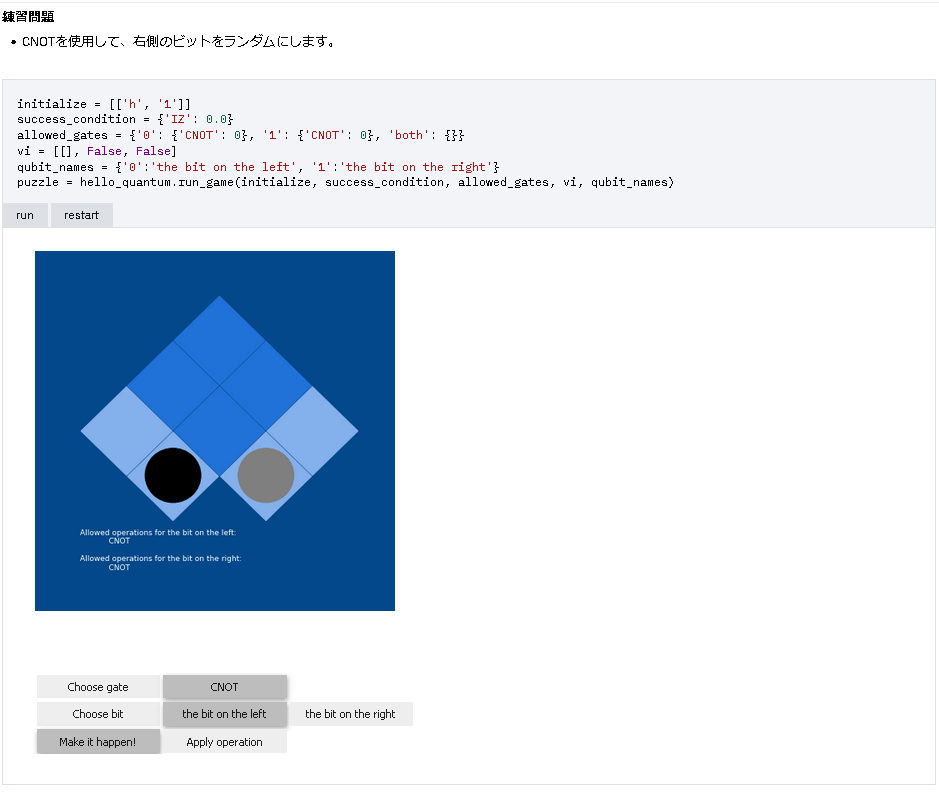
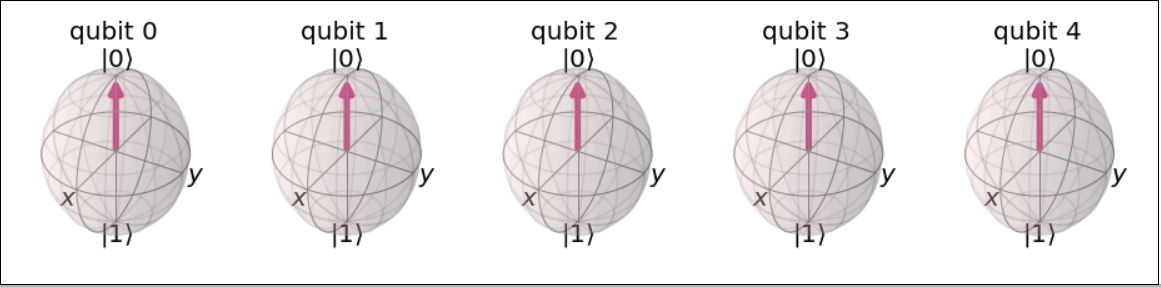
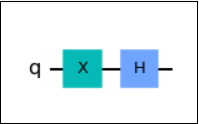
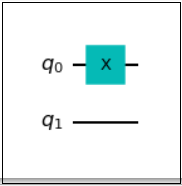
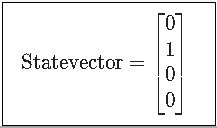
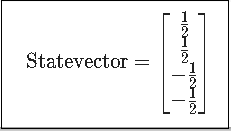
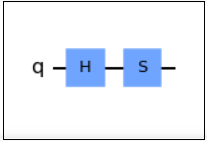
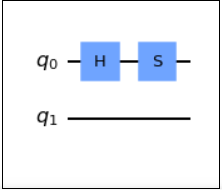
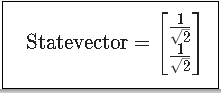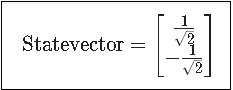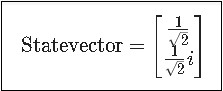概要
- Qiskit について, 学習サイト の サンプルプログラムを動かしてみた.
- 動作環境は, 学習サイト上 で行った
- 実行プログラム, 解説は, 下記の参照サイトをご覧ください
感想
- ベルンシュタイン・ヴァジラニ アルゴリズムの演算方法で, 量子オラクルについて確認してみた.
- 5 ~ 6量子ビットで確認したが出力結果が改行されなかったので, wbrタグを手動埋め込みし改行させて確認している.
- 下記の (参考)シミュレーターでの実験 の通り, ベルンシュタイン・ヴァジラニ アルゴリズム の プログラム内に, 秘密の文字列を反転する操作が実装されており, 個人的には, 手計算前に, 秘密の文字列 を 反転させる操作 と 符合すると予想する.
- 演習問題では, 10量子ビット(“1110110101”)での記述もあったが, 実行後に, エラー(Too large to display)となったため, 詳細は確認できなかったが, 5 ~ 6量子ビットで確認出来たので, 十分だと思う.
ベルンシュタイン・ヴァジラニ アルゴリズム(演習問題改題ほか)
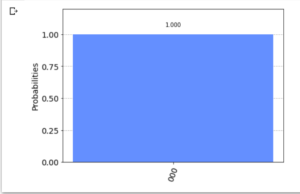
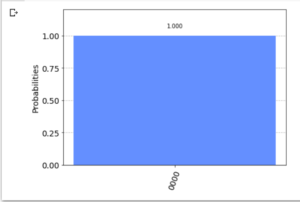
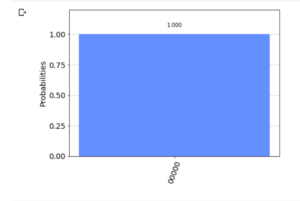
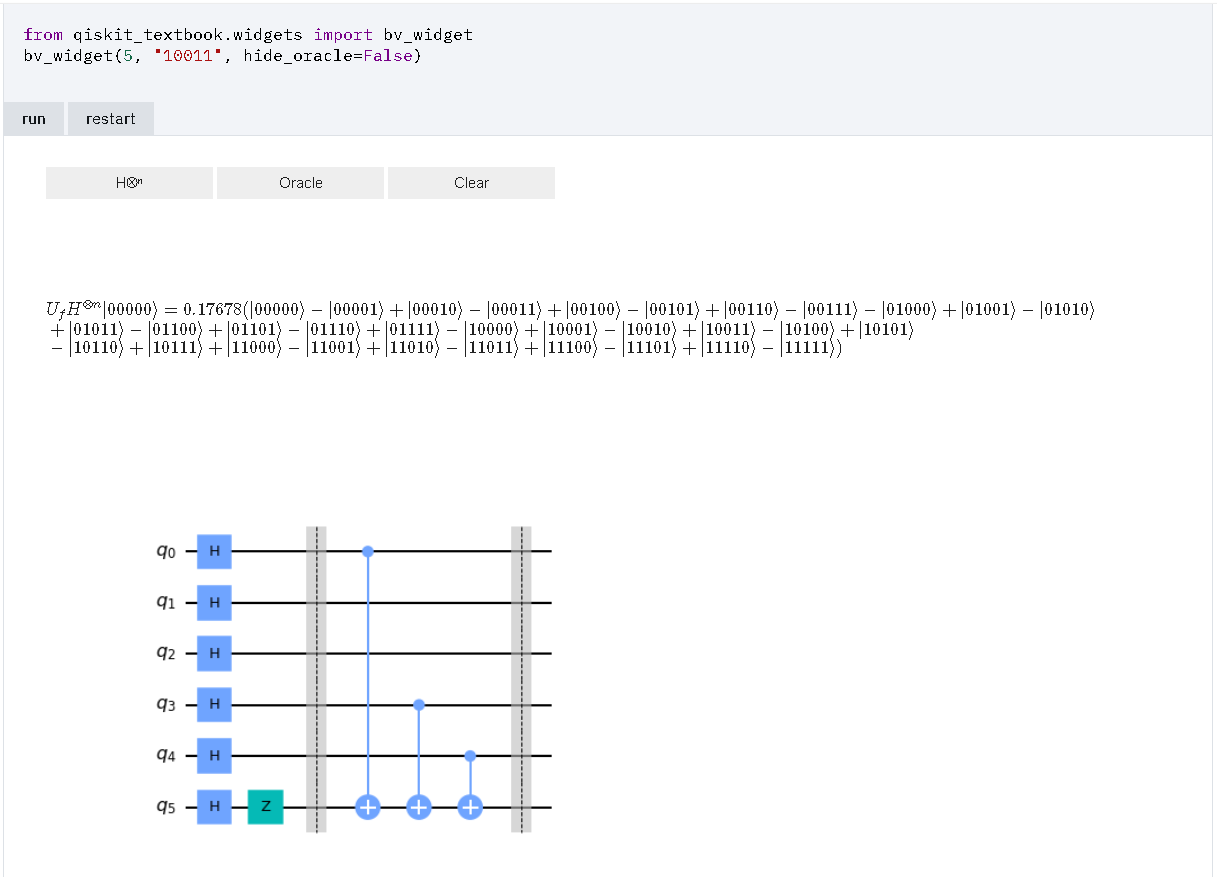
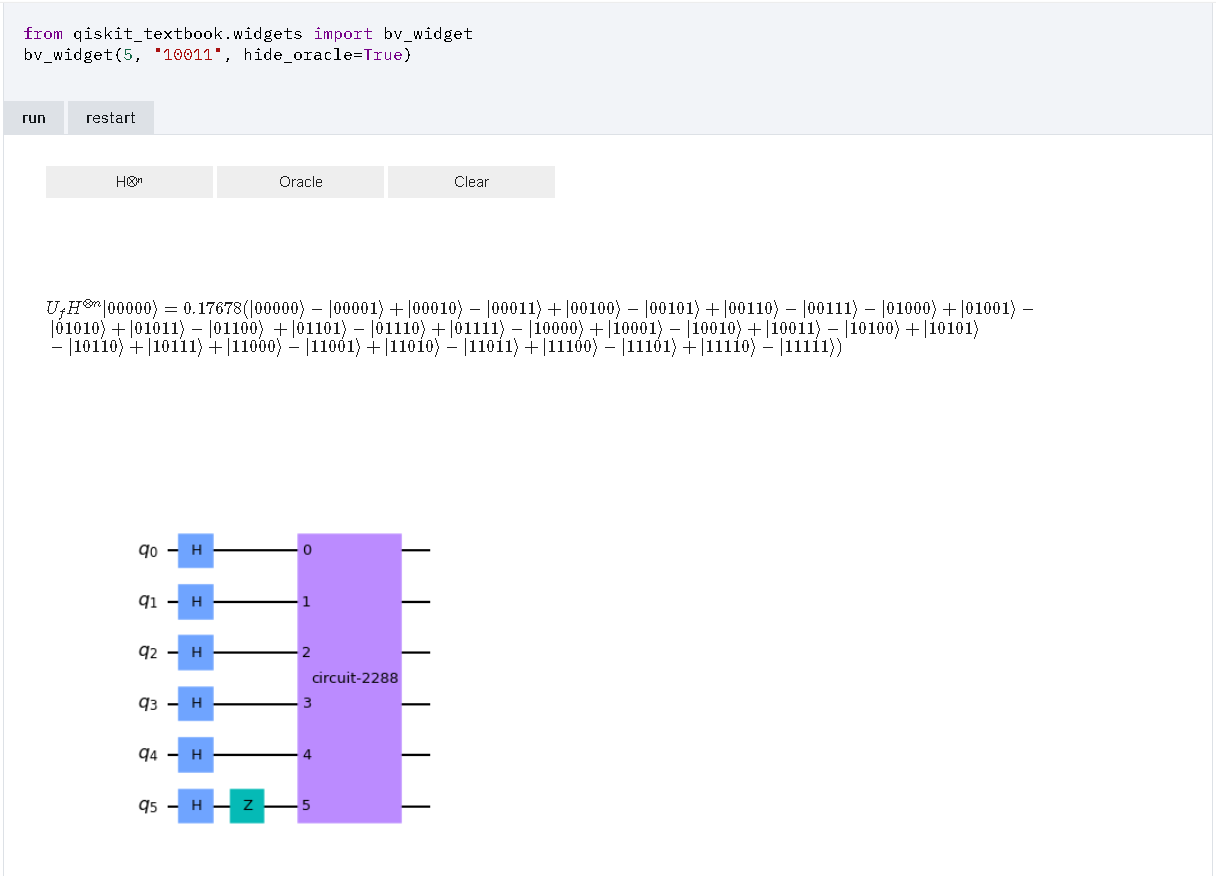
- 量子オラクル(5量子ビット “10011”)
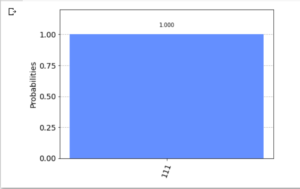
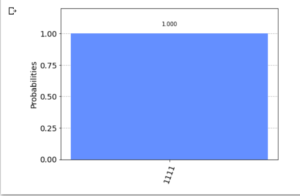
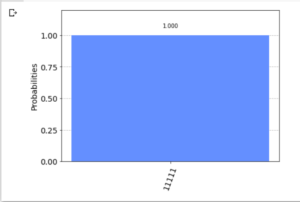
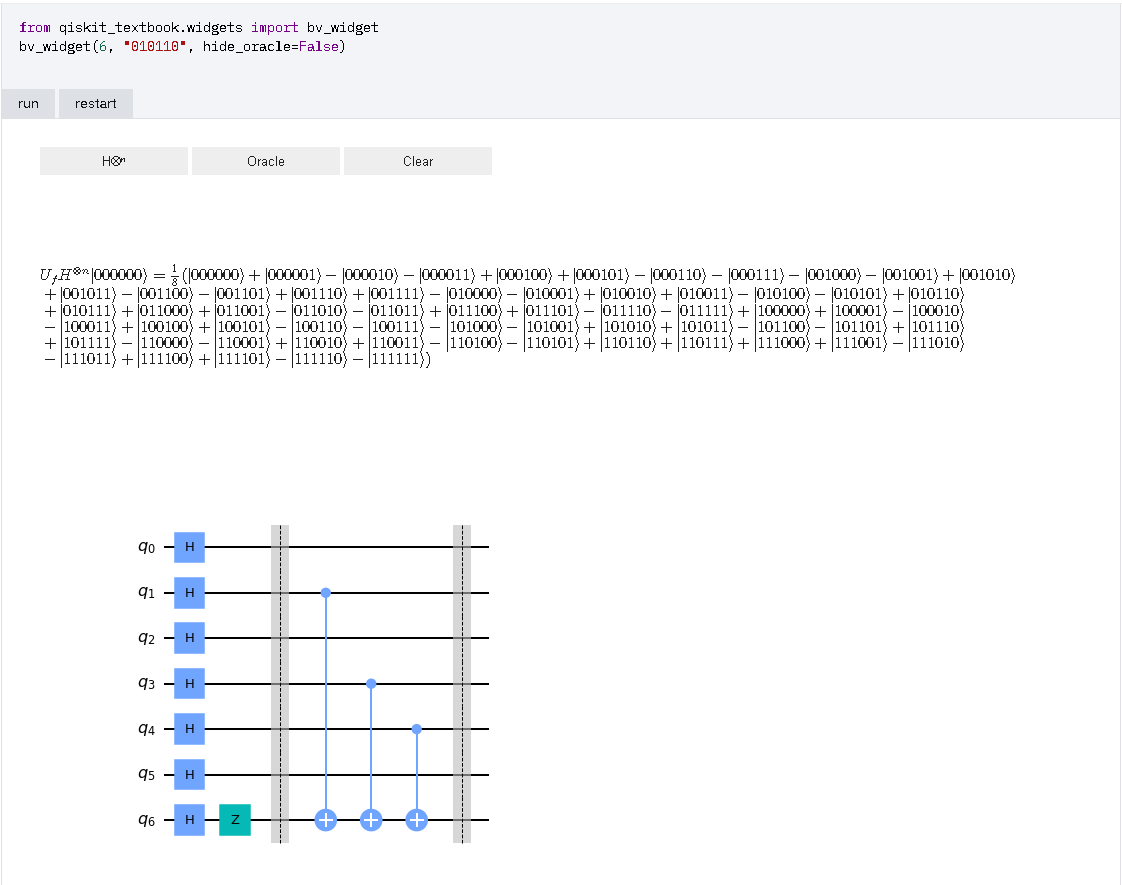
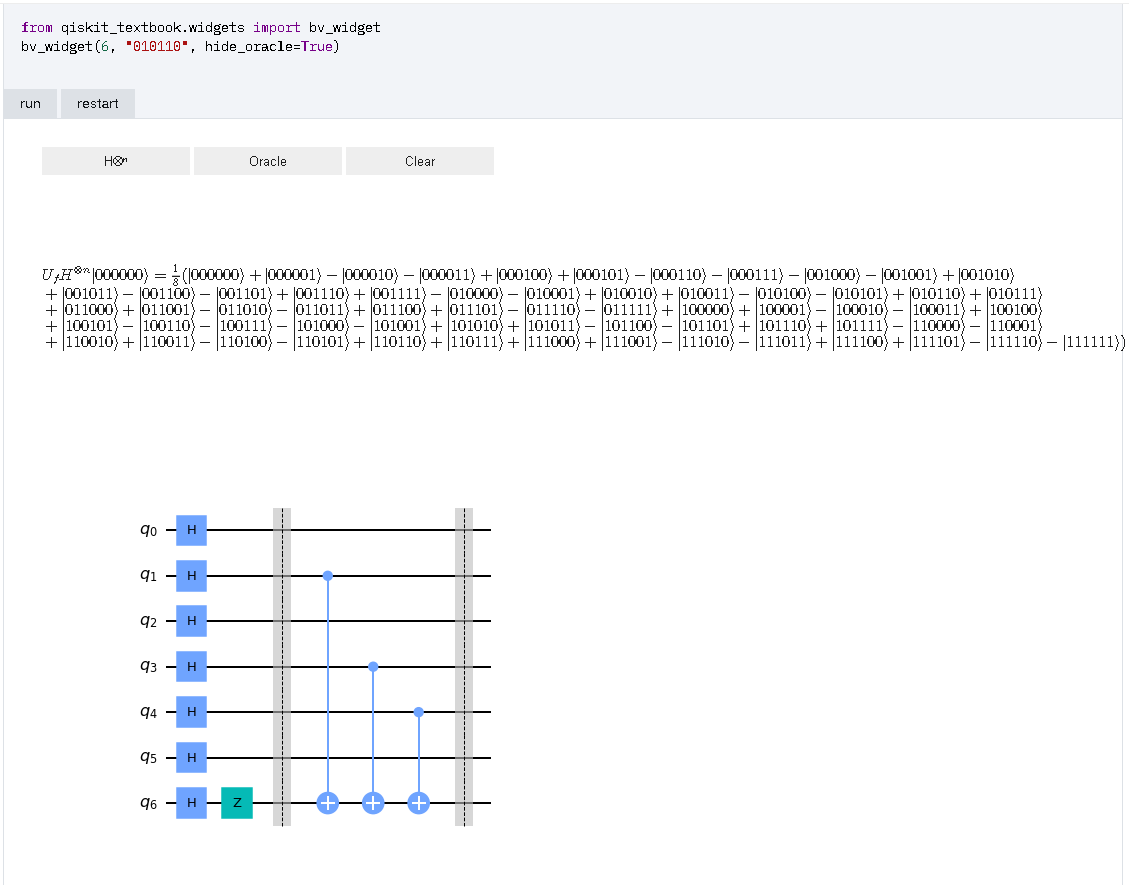
- 量子オラクル(6量子ビット “010110”)
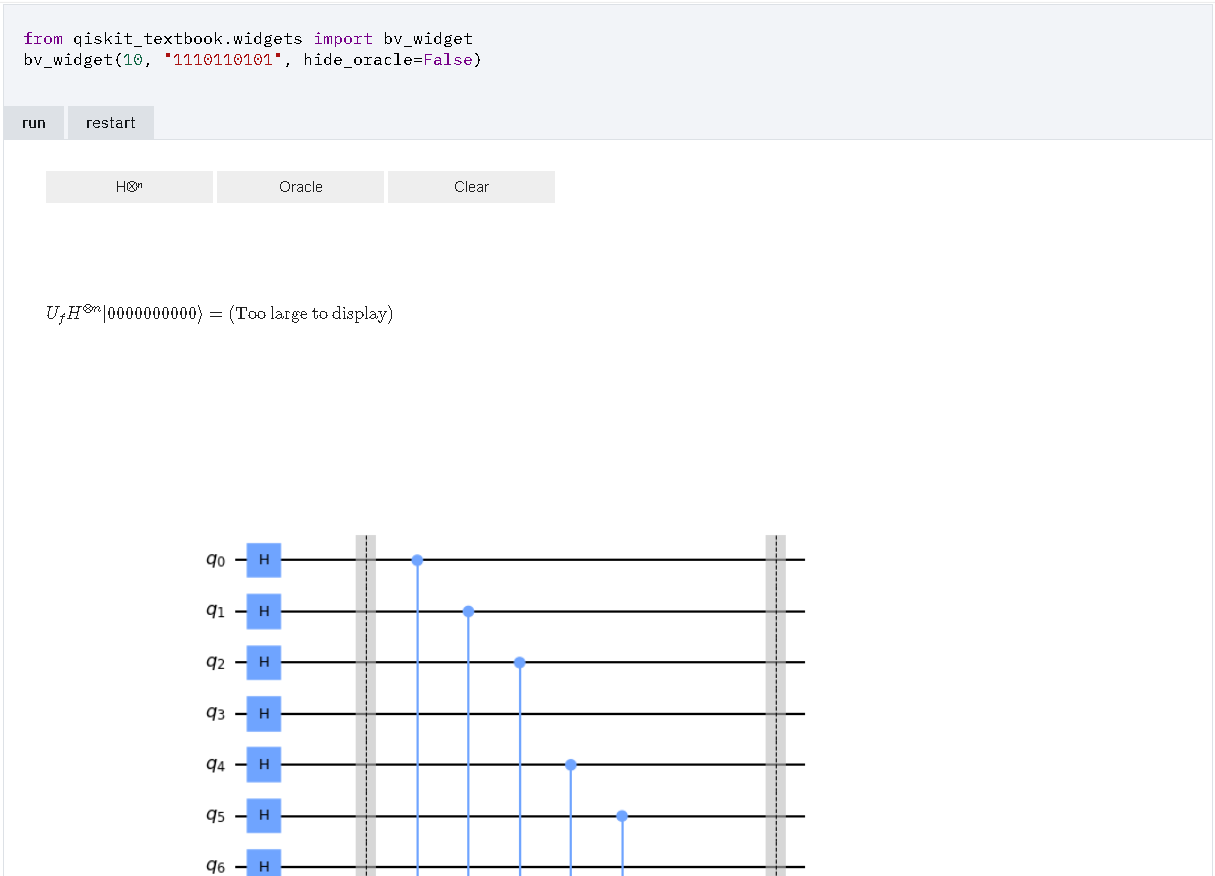
- (参考)量子オラクル(10量子ビット “1110110101”)
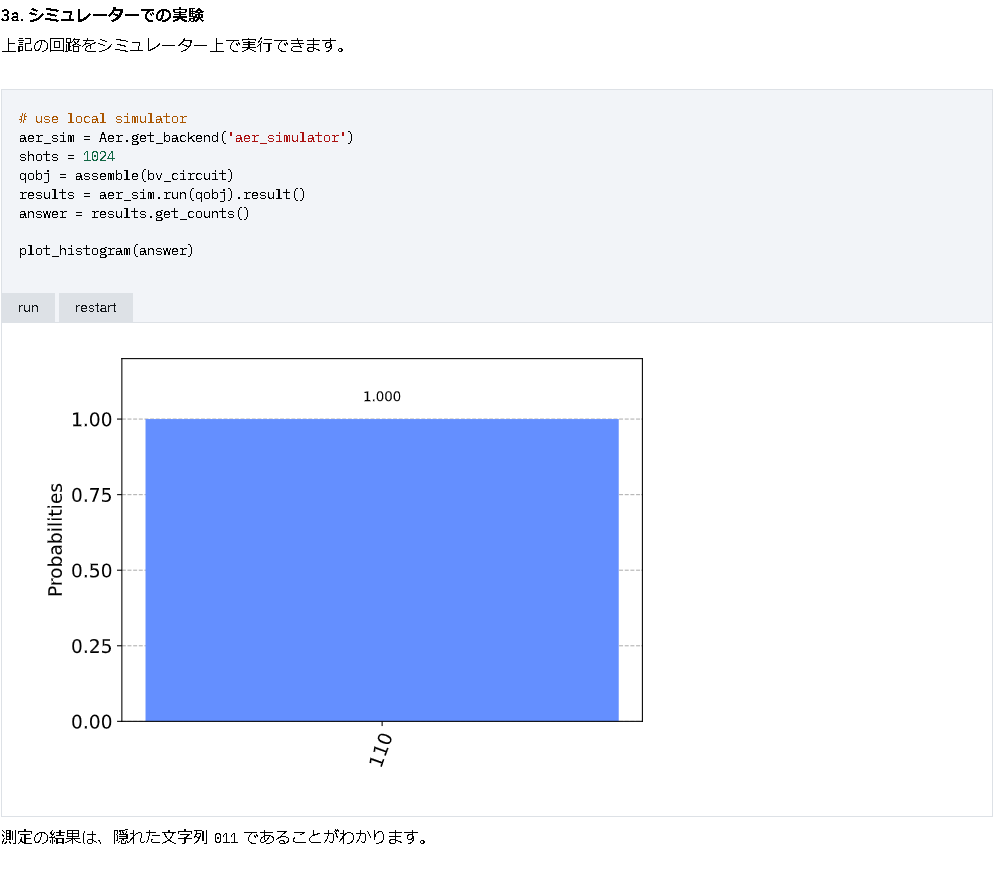
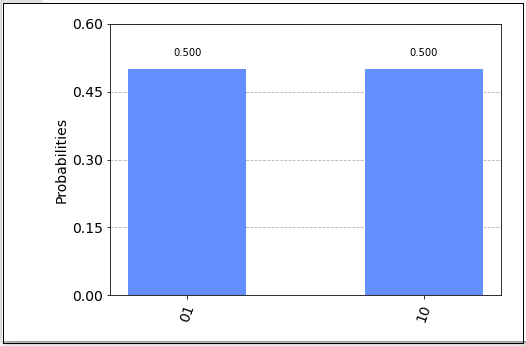
- (参考)シミュレーターでの実験
[手計算]
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 |
※ 秘密の文字列 "10011" を 反転し, "11001" と読み替えて, 計算する必要があるように見える. 1 / √32 * { (-1)(00000・11001)|00000> + (-1)(00001・11001)|00001> + (-1)(00010・11001)|00010> + (-1)(00011・11001)|00011> + (-1)(00100・11001)|00100> + (-1)(00101・11001)|00101> + (-1)(00110・11001)|00110> + (-1)(00111・11001)|00111> + (-1)(01000・11001)|01000> + (-1)(01001・11001)|01001> + (-1)(01010・11001)|01010> + (-1)(01011・11001)|01011> + (-1)(01100・11001)|01100> + (-1)(01101・11001)|01101> + (-1)(01110・11001)|01110> + (-1)(01111・11001)|01111> + (-1)(10000・11001)|10000> + (-1)(10001・11001)|10001> + (-1)(10010・11001)|10010> + (-1)(10011・11001)|10011> + (-1)(10100・11001)|10100> + (-1)(10101・11001)|10101> + (-1)(10110・11001)|10110> + (-1)(10111・11001)|10111> + (-1)(11000・11001)|11000> + (-1)(11001・11001)|11001> + (-1)(11010・11001)|11010> + (-1)(11011・11001)|11011> + (-1)(11100・11001)|11100> + (-1)(11101・11001)|11101> + (-1)(11110・11001)|11110> + (-1)(11111・11001)|11111> } ↓↓↓ 1 / √32 * { (+ |00000>) + (- |00001>) + (+ |00010>) + (- |00011>) + (+ |00100>) + (- |00101>) + (+ |00110>) + (- |00111>) + (- |01000>) + (+ |01001>) + (- |01010>) + (+ |01011>) + (- |01100>) + (+ |01101>) + (- |01110>) + (+ |01111>) + (- |10000>) + (+ |10001>) + (- |10010>) + (+ |10011>) + (- |10100>) + (+ |10101>) + (- |10110>) + (+ |10111>) + (+ |11000>) + (- |11001>) + (+ |11010>) + (- |11011>) + (+ |11100>) + (- |11101>) + (+ |11110>) + (- |11111>) } ↓↓↓ 1 / √32 * (+ |00000> - |00001> + |00010> - |00011> + |00100> - |00101> + |00110> - |00111> - |01000> + |01001> - |01010> + |01011> - |01100> + |01101> - |01110> + |01111> - |10000> + |10001> - |10010> + |10011> - |10100> + |10101> - |10110> + |10111> + |11000> - |11001> + |11010> - |11011> + |11100> - |11101> + |11110> - |11111>) 例) 11011・11001 = (左から, 1bit目どうしの積) + ... + (左から, 5bit目どうしの積) (modulo 2) = 1 * 1 + 1 * 1 + 0 * 0 + 1 * 0 + 1 * 1 (modulo 2) = 1 + 1 + 0 + 0 + 1 (modulo 2) = 3 (modulo 2) = 1 (modulo 2) → (-1) が 1個なので, -1 と 解釈. 01001・11001 = (左から, 1bit目どうしの積) + ... + (左から, 5bit目どうしの積) (modulo 2) = 0 * 1 + 1 * 1 + 0 * 0 + 0 * 0 + 1 * 1 (modulo 2) = 0 + 1 + 0 + 0 + 1 (modulo 2) = 2 (modulo 2) = 0 (modulo 2) → (-1) が 0個なので, +1 と 解釈. |
[結果]
手計算との一致を確認できた.
[手計算]
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 |
※ 秘密の文字列 "010110" を 反転し, "011010" と読み替えて, 計算する必要があるように見える. 1 / √64 * { (-1)(000000・011010)|000000> + (-1)(000001・011010)|000001> + (-1)(000010・011010)|000010> + (-1)(000011・011010)|000011> + (-1)(000100・011010)|000100> + (-1)(000101・011010)|000101> + (-1)(000110・011010)|000110> + (-1)(000111・011010)|000111> + (-1)(001000・011010)|001000> + (-1)(001001・011010)|001001> + (-1)(001010・011010)|001010> + (-1)(001011・011010)|001011> + (-1)(001100・011010)|001100> + (-1)(001101・011010)|001101> + (-1)(001110・011010)|001110> + (-1)(001111・011010)|001111> + (-1)(010000・011010)|010000> + (-1)(010001・011010)|010001> + (-1)(010010・011010)|010010> + (-1)(010011・011010)|010011> + (-1)(010100・011010)|010100> + (-1)(010101・011010)|010101> + (-1)(010110・011010)|010110> + (-1)(010111・011010)|010111> + (-1)(011000・011010)|011000> + (-1)(011001・011010)|011001> + (-1)(011010・011010)|011010> + (-1)(011011・011010)|011011> + (-1)(011100・011010)|011100> + (-1)(011101・011010)|011101> + (-1)(011110・011010)|011110> + (-1)(011111・011010)|011111> + (-1)(100000・011010)|100000> + (-1)(100001・011010)|100001> + (-1)(100010・011010)|100010> + (-1)(100011・011010)|100011> + (-1)(100100・011010)|100100> + (-1)(100101・011010)|100101> + (-1)(100110・011010)|100110> + (-1)(100111・011010)|100111> + (-1)(101000・011010)|101000> + (-1)(101001・011010)|101001> + (-1)(101010・011010)|101010> + (-1)(101011・011010)|101011> + (-1)(101100・011010)|101100> + (-1)(101101・011010)|101101> + (-1)(101110・011010)|101110> + (-1)(101111・011010)|101111> + (-1)(110000・011010)|110000> + (-1)(110001・011010)|110001> + (-1)(110010・011010)|110010> + (-1)(110011・011010)|110011> + (-1)(110100・011010)|110100> + (-1)(110101・011010)|110101> + (-1)(110110・011010)|110110> + (-1)(110111・011010)|110111> + (-1)(111000・011010)|111000> + (-1)(111001・011010)|111001> + (-1)(111010・011010)|111010> + (-1)(111011・011010)|111011> + (-1)(111100・011010)|111100> + (-1)(111101・011010)|111101> + (-1)(111110・011010)|111110> + (-1)(111111・011010)|111111> } ↓↓↓ 1 / √64 * { (+ |000000>) + (+ |000001>) + (- |000010>) + (- |000011>) + (+ |000100>) + (+ |000101>) + (- |000110>) + (- |000111>) + (- |001000>) + (- |001001>) + (+ |001010>) + (+ |001011>) + (- |001100>) + (- |001101>) + (+ |001110>) + (+ |001111>) + (- |010000>) + (- |010001>) + (+ |010010>) + (+ |010011>) + (- |010100>) + (- |010101>) + (+ |010110>) + (+ |010111>) + (+ |011000>) + (+ |011001>) + (- |011010>) + (- |011011>) + (+ |011100>) + (+ |011101>) + (- |011110>) + (- |011111>) + (+ |100000>) + (+ |100001>) + (- |100010>) + (- |100011>) + (+ |100100>) + (+ |100101>) + (- |100110>) + (- |100111>) + (- |101000>) + (- |101001>) + (+ |101010>) + (+ |101011>) + (- |101100>) + (- |101101>) + (+ |101110>) + (+ |101111>) + (- |110000>) + (- |110001>) + (+ |110010>) + (+ |110011>) + (- |110100>) + (- |110101>) + (+ |110110>) + (+ |110111>) + (+ |111000>) + (+ |111001>) + (- |111010>) + (- |111011>) + (+ |111100>) + (+ |111101>) + (- |111110>) + (- |111111>) } ↓↓↓ 1 / √64 * (+ |000000> + |000001> - |000010> - |000011> + |000100> + |000101> - |000110> - |000111> - |001000> - |001001> + |001010> + |001011> - |001100> - |001101> + |001110> + |001111> - |010000> - |010001> + |010010> + |010011> - |010100> - |010101> + |010110> + |010111> + |011000> + |011001> - |011010> - |011011> + |011100> + |011101> - |011110> - |011111> + |100000> + |100001> - |100010> - |100011> + |100100> + |100101> - |100110> - |100111> - |101000> - |101001> + |101010> + |101011> - |101100> - |101101> + |101110> + |101111> - |110000> - |110001> + |110010> + |110011> - |110100> - |110101> + |110110> + |110111> + |111000> + |111001> - |111010> - |111011> + |111100> + |111101> - |111110> - |111111>) 例) 011011・011010 = (左から, 1bit目どうしの積) + ... + (左から, 6bit目どうしの積) (modulo 2) = 0 * 0 + 1 * 1 + 1 * 1 + 0 * 0 + 1 * 1 + 1 * 0 (modulo 2) = 0 + 1 + 1 + 0 + 1 + 0 (modulo 2) = 3 (modulo 2) = 1 (modulo 2) → (-1) が 1個なので, -1 と 解釈. 011100・011010 = (左から, 1bit目どうしの積) + ... + (左から, 6bit目どうしの積) (modulo 2) = 0 * 0 + 1 * 1 + 1 * 1 + 1 * 0 + 0 * 1 + 0 * 0 (modulo 2) = 0 + 1 + 1 + 0 + 0 + 0 (modulo 2) = 2 (modulo 2) = 0 (modulo 2) → (-1) が 0個なので, +1 と 解釈. |
[結果]
手計算との一致を確認できた.
[結果]
エラー出力された.
公式サイトでは, 秘密の文字列 “011” で, シミュレーターによる実験を見ることが出来る.
⇒ プログラム中に, 以下の実装箇所があるが, これをコメントアウト(秘密の文字列の反転を行わない)して, 結果を確認してみる.
|
1 2 3 |
~ (略) ~ s = s[::-1] # reverse s to fit qiskit's qubit ordering ~ (略) ~ |
[結果]
シミュレーター の 結果が, 秘密の文字列 “110” で, 出力されることを確認できた.