概要
- Qiskit について, 学習サイト の サンプルプログラムを動かしてみた.
- 動作環境は, 学習サイト上 で行った
- 実行プログラム, 解説は, 下記の参照サイトをご覧ください
感想
- ベルンシュタイン・ヴァジラニ アルゴリズムの演算方法で, 量子オラクルについて確認してみた.
- 既に, 学習環境が用意されており, 数値を書き換えるなどして試行錯誤もできるので, 個人的には, 非常に面白く感じた.
ベルンシュタイン・ヴァジラニ アルゴリズム
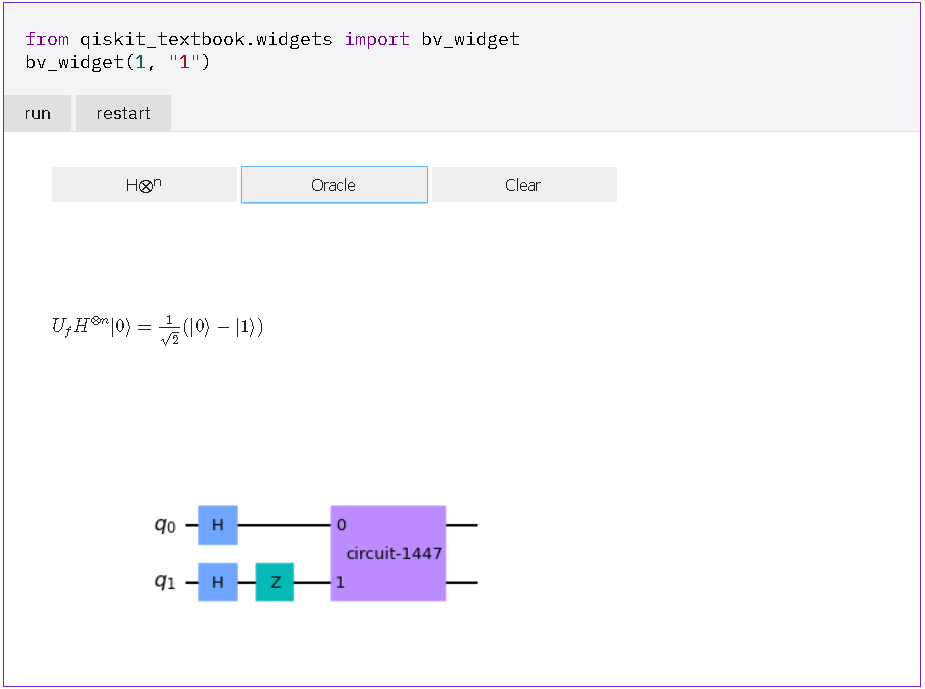
- 量子オラクル(1量子ビット “1”)
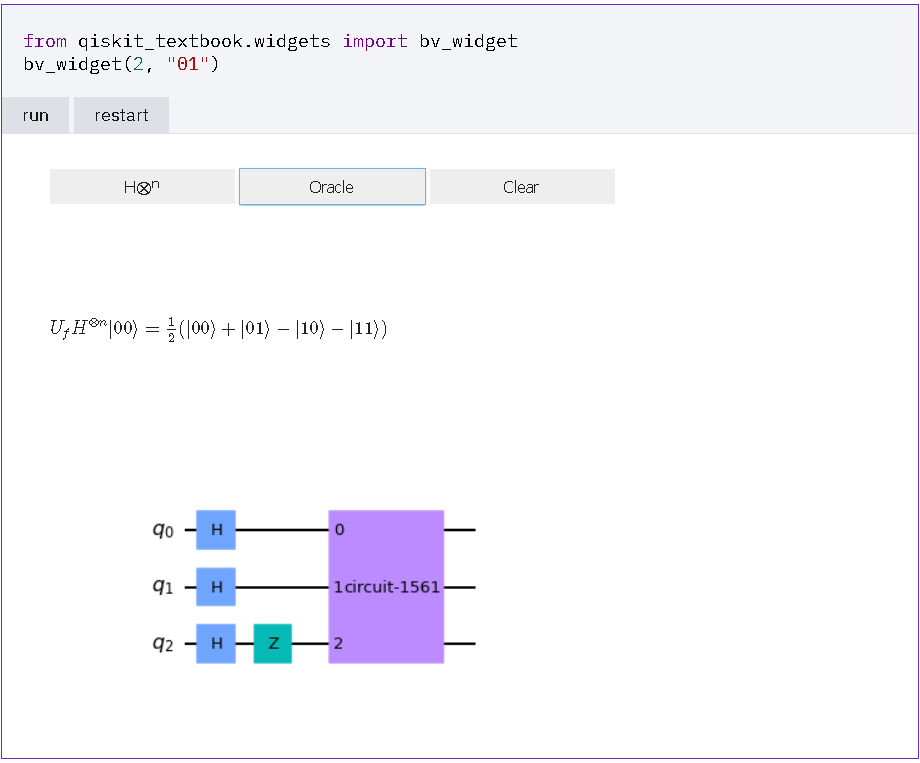
- 量子オラクル(2量子ビット “01”)
- 量子オラクル(3量子ビット “110”)
- 量子オラクル(4量子ビット “1011”)
[手計算]
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
1 / √2 * { (-1)(0・1)|0> + (-1)(1・1)|1> + ↓↓↓ 1 / √2 * { (+ |0>) + (- |1>) } ↓↓↓ 1 / √2 * (+ |0> - |1>) 例) 0・1 = (左から, 1bit目どうしの積) = 0 * 1 = 0 (modulo 2) → (-1) が 0個なので, +1 と 解釈. |
[結果]
手計算との一致を確認できた.
[手計算]
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
※ 秘密の文字列 "01" を 反転し, "10" と読み替えて, 計算する必要があるように見える. 1 / √4 * { (-1)(00・10)|00> + (-1)(01・10)|01> + (-1)(10・10)|10> + (-1)(11・10)|11> + } ↓↓↓ 1 / √4 * { (+ |00>) + (+ |01>) + (- |10>) + (- |11>) + } ↓↓↓ 1 / √4 * (+ |00> + |01> - |10> - |11>) 例) 01・10 = (左から, 1bit目どうしの積) + (左から, 2bit目どうしの積) (modulo 2) = 0 * 1 + 1 * 0 (modulo 2) = 0 + 0 (modulo 2) = 0 (modulo 2) → (-1) が 0個なので, +1 と 解釈. 11・10 = (左から, 1bit目どうしの積) + (左から, 2bit目どうしの積) (modulo 2) = 1 * 1 + 1 * 0 (modulo 2) = 1 + 0 (modulo 2) = 1 (modulo 2) → (-1) が 1個なので, -1 と 解釈. |
[結果]
手計算との一致を確認できた.
[手計算]
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
※ 秘密の文字列 "110" を 反転し, "011" と読み替えて, 計算する必要があるように見える. 1 / √8 * { (-1)(000・011)|000> + (-1)(001・011)|001> + (-1)(010・011)|010> + (-1)(011・011)|011> + (-1)(100・011)|100> + (-1)(101・011)|101> + (-1)(110・011)|110> + (-1)(111・011)|111> } ↓↓↓ 1 / √8 * { (+ |000>) + (- |001>) + (- |010>) + (+ |011>) + (+ |100>) + (- |101>) + (- |110>) + (+ |111>) } ↓↓↓ 1 / √8 * (+ |000> - |001> - |010> + |011> + |100> - |101> - |110> + |111>) 例) 010・011 = (左から, 1bit目どうしの積) + (左から, 2bit目どうしの積) + (左から, 3bit目どうしの積) (modulo 2) = 0 * 0 + 1 * 1 + 0 * 1 (modulo 2) = 0 + 1 + 0 (modulo 2) = 1 (modulo 2) → (-1) が 1個なので, -1 と 解釈. 100・011 = (左から, 1bit目どうしの積) + (左から, 2bit目どうしの積) + (左から, 3bit目どうしの積) (modulo 2) = 1 * 0 + 0 * 1 + 0 * 1 (modulo 2) = 0 + 0 + 0 (modulo 2) = 0 (modulo 2) → (-1) が 0個なので, +1 と 解釈. |
[結果]
手計算との一致を確認できた.

[手計算]
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 |
※ 秘密の文字列 "1011" を 反転し, "1101" と読み替えて, 計算する必要があるように見える. 1 / √16 * { (-1)(0000・1101)|0000> + (-1)(0001・1101)|0001> + (-1)(0010・1101)|0010> + (-1)(0011・1101)|0011> + (-1)(0100・1101)|0100> + (-1)(0101・1101)|0101> + (-1)(0110・1101)|0110> + (-1)(0111・1101)|0111> + (-1)(1000・1101)|1000> + (-1)(1001・1101)|1001> + (-1)(1010・1101)|1010> + (-1)(1011・1101)|1011> + (-1)(1100・1101)|1100> + (-1)(1101・1101)|1101> + (-1)(1110・1101)|1110> + (-1)(1111・1101)|1111> } ↓↓↓ 1 / √16 * { (+ |0000>) + (- |0001>) + (+ |0010>) + (- |0011>) + (- |0100>) + (+ |0101>) + (- |0110>) + (+ |0111>) + (- |1000>) + (+ |1001>) + (- |1010>) + (+ |1011>) + (+ |1100>) + (- |1101>) + (+ |1110>) + (- |1111>) } ↓↓↓ 1 / √16 * (+ |0000> - |0001> + |0010> - |0011> - |0100> + |0101> - |0110> + |0111> - |1000> + |1001> - |1010> + |1011> + |1100> - |1101> + |1110> - |1111>) 例) 0111・1101 = (左から, 1bit目どうしの積) + (左から, 2bit目どうしの積) + (左から, 3bit目どうしの積) + (左から, 4bit目どうしの積) (modulo 2) = 0 * 1 + 1 * 1 + 1 * 0 + 1 * 1 (modulo 2) = 0 + 1 + 0 + 1 (modulo 2) = 2 (modulo 2) = 0 (modulo 2) → (-1) が 0個なので, +1 と 解釈. 1101・1101 = (左から, 1bit目どうしの積) + (左から, 2bit目どうしの積) + (左から, 3bit目どうしの積) + (左から, 4bit目どうしの積) (modulo 2) = 1 * 1 + 1 * 1 + 0 * 0 + 1 * 1 (modulo 2) = 1 + 1 + 0 + 1 (modulo 2) = 3 (modulo 2) = 1 (modulo 2) → (-1) が 1個なので, -1 と 解釈. |
[結果]
手計算との一致を確認できた.

