概要
- Qiskit について, 学習サイト の サンプルプログラムを動かしてみた.
- 動作環境は, Google Colaboratory で行った
- 実行プログラム, 解説は, 下記の参照サイトをご覧ください
感想
- 本家のサイトの学習教材が非常に詳しいので, 今後も, 時間を見つけて, 確認していこうと思う.
ドイチ-ジョサ(Deutsch-Jozsa)のアルゴリズム(演習問題)
- 本家のサイトにある, dj_oracle関数をベースに, 演習問題用のオラクルを実装してみた.
- 具体的には, n が, 1 ~ 4 で 分布型, 5 で 定値型 となるようにしている.
- 出力結果(量子回路)については, n = 1 ~ 5 で 同じ内容が出力されたと理解する.
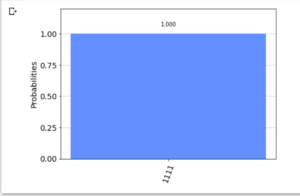
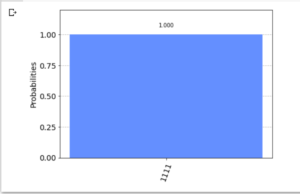
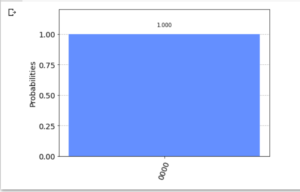
- グラフ(添付画像)については, n = 1 ~ 4 で ‘1111’ が, 100%, n = 5 で ‘0000’ が 100% だった.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
# initialization import numpy as np # importing Qiskit from qiskit import IBMQ, Aer from qiskit.providers.ibmq import least_busy from qiskit import QuantumCircuit, assemble, transpile # import basic plot tools from qiskit.visualization import plot_histogram # n is between 1 and 5. def dj_problem_oracle(n): # We need to make a QuantumCircuit object to return # This circuit has 5 qubits: the input size is 5, plus one output qubit. oracle_qc = QuantumCircuit(5) # Try changing the location of the X gate depending on the value of n. # If n is 4 or less, make the X gate act on the bit at the corresponding location. if n in [(i + 1) for i in range(4)]: oracle_qc.x(n - 1) # Controlled-NOT gates for qubit in range(4): oracle_qc.cx(qubit, 4) # If n is 5, do nothing if n == 5: pass # Convert to quantum gate. oracle_gate = oracle_qc.to_gate() # To show when we display the circuit. oracle_gate.name = "Deutsch-Jozsa Problem Oracle" # Return a quantum gate. return oracle_gate # This function (dj_algorithm) quotes the contents of the following site. # https://qiskit.org/textbook/ja/ch-algorithms/deutsch-jozsa.html def dj_algorithm(oracle): dj_circuit = QuantumCircuit(5, 4) # Set up the output qubit: dj_circuit.x(4) dj_circuit.h(4) # And set up the input register: for qubit in range(4): dj_circuit.h(qubit) # Let's append the oracle gate to our circuit: dj_circuit.append(oracle, range(5)) # Finally, perform the H-gates again and measure: for qubit in range(4): dj_circuit.h(qubit) for i in range(4): dj_circuit.measure(i, i) return dj_circuit # oracle_gate = dj_problem_oracle(1) # oracle_gate = dj_problem_oracle(2) # oracle_gate = dj_problem_oracle(3) # oracle_gate = dj_problem_oracle(4) oracle_gate = dj_problem_oracle(5) dj_circuit = dj_algorithm(oracle_gate) dj_circuit.draw() |
- 出力結果(量子回路, n = 1)
- 出力結果(量子回路, n = 2)
- 出力結果(量子回路, n = 3)
- 出力結果(量子回路, n = 4)
- 出力結果(量子回路, n = 5)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
┌───┐ ┌───────────────────────────────┐┌───┐┌─┐ q_0: ┤ H ├─────┤0 ├┤ H ├┤M├───────── ├───┤ │ │├───┤└╥┘┌─┐ q_1: ┤ H ├─────┤1 ├┤ H ├─╫─┤M├────── ├───┤ │ │├───┤ ║ └╥┘┌─┐ q_2: ┤ H ├─────┤2 Deutsch-Jozsa Problem Oracle ├┤ H ├─╫──╫─┤M├─── ├───┤ │ │├───┤ ║ ║ └╥┘┌─┐ q_3: ┤ H ├─────┤3 ├┤ H ├─╫──╫──╫─┤M├ ├───┤┌───┐│ │└───┘ ║ ║ ║ └╥┘ q_4: ┤ X ├┤ H ├┤4 ├──────╫──╫──╫──╫─ └───┘└───┘└───────────────────────────────┘ ║ ║ ║ ║ c: 4/═════════════════════════════════════════════════╩══╩══╩══╩═ 0 1 2 3 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
┌───┐ ┌───────────────────────────────┐┌───┐┌─┐ q_0: ┤ H ├─────┤0 ├┤ H ├┤M├───────── ├───┤ │ │├───┤└╥┘┌─┐ q_1: ┤ H ├─────┤1 ├┤ H ├─╫─┤M├────── ├───┤ │ │├───┤ ║ └╥┘┌─┐ q_2: ┤ H ├─────┤2 Deutsch-Jozsa Problem Oracle ├┤ H ├─╫──╫─┤M├─── ├───┤ │ │├───┤ ║ ║ └╥┘┌─┐ q_3: ┤ H ├─────┤3 ├┤ H ├─╫──╫──╫─┤M├ ├───┤┌───┐│ │└───┘ ║ ║ ║ └╥┘ q_4: ┤ X ├┤ H ├┤4 ├──────╫──╫──╫──╫─ └───┘└───┘└───────────────────────────────┘ ║ ║ ║ ║ c: 4/═════════════════════════════════════════════════╩══╩══╩══╩═ 0 1 2 3 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
┌───┐ ┌───────────────────────────────┐┌───┐┌─┐ q_0: ┤ H ├─────┤0 ├┤ H ├┤M├───────── ├───┤ │ │├───┤└╥┘┌─┐ q_1: ┤ H ├─────┤1 ├┤ H ├─╫─┤M├────── ├───┤ │ │├───┤ ║ └╥┘┌─┐ q_2: ┤ H ├─────┤2 Deutsch-Jozsa Problem Oracle ├┤ H ├─╫──╫─┤M├─── ├───┤ │ │├───┤ ║ ║ └╥┘┌─┐ q_3: ┤ H ├─────┤3 ├┤ H ├─╫──╫──╫─┤M├ ├───┤┌───┐│ │└───┘ ║ ║ ║ └╥┘ q_4: ┤ X ├┤ H ├┤4 ├──────╫──╫──╫──╫─ └───┘└───┘└───────────────────────────────┘ ║ ║ ║ ║ c: 4/═════════════════════════════════════════════════╩══╩══╩══╩═ 0 1 2 3 |

|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
┌───┐ ┌───────────────────────────────┐┌───┐┌─┐ q_0: ┤ H ├─────┤0 ├┤ H ├┤M├───────── ├───┤ │ │├───┤└╥┘┌─┐ q_1: ┤ H ├─────┤1 ├┤ H ├─╫─┤M├────── ├───┤ │ │├───┤ ║ └╥┘┌─┐ q_2: ┤ H ├─────┤2 Deutsch-Jozsa Problem Oracle ├┤ H ├─╫──╫─┤M├─── ├───┤ │ │├───┤ ║ ║ └╥┘┌─┐ q_3: ┤ H ├─────┤3 ├┤ H ├─╫──╫──╫─┤M├ ├───┤┌───┐│ │└───┘ ║ ║ ║ └╥┘ q_4: ┤ X ├┤ H ├┤4 ├──────╫──╫──╫──╫─ └───┘└───┘└───────────────────────────────┘ ║ ║ ║ ║ c: 4/═════════════════════════════════════════════════╩══╩══╩══╩═ 0 1 2 3 |

|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
┌───┐ ┌───────────────────────────────┐┌───┐┌─┐ q_0: ┤ H ├─────┤0 ├┤ H ├┤M├───────── ├───┤ │ │├───┤└╥┘┌─┐ q_1: ┤ H ├─────┤1 ├┤ H ├─╫─┤M├────── ├───┤ │ │├───┤ ║ └╥┘┌─┐ q_2: ┤ H ├─────┤2 Deutsch-Jozsa Problem Oracle ├┤ H ├─╫──╫─┤M├─── ├───┤ │ │├───┤ ║ ║ └╥┘┌─┐ q_3: ┤ H ├─────┤3 ├┤ H ├─╫──╫──╫─┤M├ ├───┤┌───┐│ │└───┘ ║ ║ ║ └╥┘ q_4: ┤ X ├┤ H ├┤4 ├──────╫──╫──╫──╫─ └───┘└───┘└───────────────────────────────┘ ║ ║ ║ ║ c: 4/═════════════════════════════════════════════════╩══╩══╩══╩═ 0 1 2 3 |
補足
- 上記だけだと分かりづらい印象があったため, dj_problem_oracle関数内の量子回路(オラクル)も確認した.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
# initialization import numpy as np # importing Qiskit from qiskit import IBMQ, Aer from qiskit.providers.ibmq import least_busy from qiskit import QuantumCircuit, assemble, transpile # import basic plot tools from qiskit.visualization import plot_histogram # n is between 1 and 5. def dj_problem_oracle(n): # We need to make a QuantumCircuit object to return # This circuit has 5 qubits: the input size is 5, plus one output qubit. oracle_qc = QuantumCircuit(5) # Try changing the location of the X gate depending on the value of n. # If n is 4 or less, make the X gate act on the bit at the corresponding location. if n in [(i + 1) for i in range(4)]: oracle_qc.x(n - 1) # Controlled-NOT gates for qubit in range(4): oracle_qc.cx(qubit, 4) # If n is 5, do nothing if n == 5: pass # Return a QuantumCircuit. return oracle_qc # oracle_qc = dj_problem_oracle(1) # oracle_qc = dj_problem_oracle(2) # oracle_qc = dj_problem_oracle(3) # oracle_qc = dj_problem_oracle(4) oracle_qc = dj_problem_oracle(5) oracle_qc.draw() |
- 出力結果(オラクル/量子回路, n = 1)
- 出力結果(オラクル/量子回路, n = 2)
- 出力結果(オラクル/量子回路, n = 3)
- 出力結果(オラクル/量子回路, n = 4)
- 出力結果(オラクル/量子回路, n = 5)
|
1 2 3 4 5 6 7 8 9 10 11 |
┌───┐ q_0: ┤ X ├──■───────────────── └───┘ │ q_1: ───────┼────■──────────── │ │ q_2: ───────┼────┼────■─────── │ │ │ q_3: ───────┼────┼────┼────■── ┌─┴─┐┌─┴─┐┌─┴─┐┌─┴─┐ q_4: ─────┤ X ├┤ X ├┤ X ├┤ X ├ └───┘└───┘└───┘└───┘ |
|
1 2 3 4 5 6 7 8 9 10 |
q_0: ───────■───────────────── ┌───┐ │ q_1: ┤ X ├──┼────■──────────── └───┘ │ │ q_2: ───────┼────┼────■─────── │ │ │ q_3: ───────┼────┼────┼────■── ┌─┴─┐┌─┴─┐┌─┴─┐┌─┴─┐ q_4: ─────┤ X ├┤ X ├┤ X ├┤ X ├ └───┘└───┘└───┘└───┘ |
|
1 2 3 4 5 6 7 8 9 10 |
q_0: ───────■───────────────── │ q_1: ───────┼────■──────────── ┌───┐ │ │ q_2: ┤ X ├──┼────┼────■─────── └───┘ │ │ │ q_3: ───────┼────┼────┼────■── ┌─┴─┐┌─┴─┐┌─┴─┐┌─┴─┐ q_4: ─────┤ X ├┤ X ├┤ X ├┤ X ├ └───┘└───┘└───┘└───┘ |
|
1 2 3 4 5 6 7 8 9 10 |
q_0: ───────■───────────────── │ q_1: ───────┼────■──────────── │ │ q_2: ───────┼────┼────■─────── ┌───┐ │ │ │ q_3: ┤ X ├──┼────┼────┼────■── └───┘┌─┴─┐┌─┴─┐┌─┴─┐┌─┴─┐ q_4: ─────┤ X ├┤ X ├┤ X ├┤ X ├ └───┘└───┘└───┘└───┘ |
|
1 2 3 4 5 6 7 8 9 |
q_0: q_1: q_2: q_3: q_4: |
